математическое моделирование доменного процесса

Математическое моделирование доменного процесса – это мощный инструмент, позволяющий оптимизировать производство чугуна и повысить его качество. Модели позволяют анализировать влияние различных факторов на процесс, прогнозировать поведение системы и разрабатывать эффективные стратегии управления.

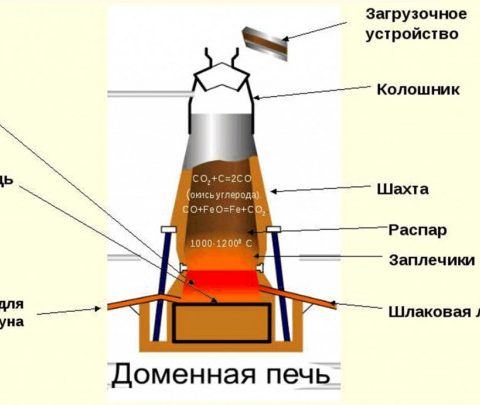
Доменный процесс – это сложный и многогранный технологический процесс, лежащий в основе производства чугуна, являющегося ключевым материалом для металлургической промышленности. Он включает в себя множество физических и химических явлений, происходящих в сложных условиях высоких температур и давлений. Для глубокого понимания и управления этим процессом, а также для оптимизации производства чугуна с заданными свойствами, необходимо использовать методы математического моделирования.

Математическое моделирование доменного процесса позволяет создавать виртуальные модели, которые имитируют реальные процессы, происходящие в доменной печи. Эти модели основаны на фундаментальных законах физики и химии, а также на эмпирических данных, полученных в ходе экспериментов и наблюдений. Благодаря математическому моделированию можно⁚

• Анализировать влияние различных факторов на процесс плавки.
• Прогнозировать поведение системы при изменении технологических параметров.
• Разрабатывать эффективные стратегии управления процессом.
• Оптимизировать технологические параметры для получения чугуна с заданными свойствами.
• Снизить затраты на производство и повысить эффективность процесса.

В последние годы математическое моделирование доменного процесса активно развивается, что обусловлено появлением новых мощных вычислительных инструментов и развитием методов математического моделирования. Современные модели доменного процесса представляют собой сложные системы уравнений, которые описывают тепломассоперенос, химические реакции, гидродинамику и другие процессы, происходящие в печи. Эти модели позволяют получать более точные прогнозы и более эффективно управлять процессом плавки.

Основные этапы моделирования

Математическое моделирование доменного процесса – это комплексный подход, включающий в себя несколько ключевых этапов, которые последовательно реализуются для достижения поставленных целей. Эти этапы тесно связаны между собой и обеспечивают последовательное построение и развитие модели.

1. Формулировка задачи. На этом этапе определяются цели моделирования, выбираются ключевые параметры, которые необходимо учитывать в модели, и определяется уровень детализации модели. Важно четко сформулировать вопросы, на которые должна ответить модель.
2. Сбор и обработка данных. Для создания реалистичной модели необходимо собрать достаточное количество данных о процессе. Эти данные могут быть получены из реальных экспериментов, из литературных источников, а также из других источников. Данные должны быть обработаны и проанализированы для выявления зависимостей и особенностей процесса.
3. Выбор математического аппарата. На этом этапе определяется тип модели, ее структура, а также выбираются математические уравнения, которые будут использоваться для описания процесса. Выбор математического аппарата зависит от целей моделирования, от уровня детализации модели, а также от доступных вычислительных ресурсов.
4. Разработка модели. На этом этапе создается собственно модель доменного процесса. Модель представляет собой систему уравнений, которая описывает физические и химические процессы, происходящие в доменной печи. Модель может быть статической или динамической, в зависимости от целей моделирования.
5. Проверка и валидация модели. После создания модели необходимо проверить ее точность и валидность. Для этого модель сравнивается с реальными данными, полученными в ходе экспериментов или наблюдений. В случае несоответствия модель может быть модифицирована или переделана.
6. Применение модели. После проверки и валидации модель может быть использована для решения практических задач, например, для оптимизации технологических параметров плавки, для прогнозирования поведения системы при изменении условий плавки, а также для разработки новых технологий производства чугуна.

Каждый из этих этапов является неотъемлемой частью процесса моделирования и требует тщательного подхода. Только при правильной организации и реализации всех этапов можно получить достоверную и практически применимую модель доменного процесса.

Методы математического моделирования

Для создания математических моделей доменного процесса используются различные методы, каждый из которых имеет свои преимущества и недостатки. Выбор метода зависит от целей моделирования, от уровня детализации модели, а также от доступных вычислительных ресурсов.

• Дифференциальные уравнения. Этот метод основан на использовании системы дифференциальных уравнений, которые описывают изменение состояния системы во времени. Дифференциальные уравнения широко используются для моделирования физических и химических процессов, происходящих в доменной печи. Этот метод позволяет учитывать взаимодействие между разными компонентами системы и моделировать динамические процессы.
• Метод конечных элементов. Этот метод основан на разбиении области моделирования на небольшие элементы и решении системы уравнений для каждого элемента. Метод конечных элементов позволяет учитывать геометрическую сложность доменной печи и моделировать неравномерное распределение температуры, давления и других параметров в разных точках системы.
• Статистические методы. Статистические методы используются для анализа экспериментальных данных и для построения эмпирических моделей. Эти методы позволяют установить зависимости между входными и выходными параметрами системы и предсказать поведение системы при изменении условий плавки. Статистические методы особенно эффективны при отсутствии полной информации о физических и химических процессах, происходящих в доменной печи.
• Метод искусственных нейронных сетей. Искусственные нейронные сети являются мощным инструментом для моделирования сложных нелинейных систем. Они способны обучаться на больших наборах данных и предсказывать поведение системы при изменении условий плавки. Этот метод особенно эффективен для моделирования процессов, механизмы которых не полностью поняты.

Выбор конкретного метода моделирования зависит от конкретной задачи и от доступных ресурсов. Часто используются комбинированные методы, которые позволяют учитывать разные аспекты доменного процесса и создавать более точные и практически применимые модели.